NAND or a NAND gate is a term found in digital electronics. It refers to a logic gate that produces a specific result. Results are always put out in binary, meaning there are only two possible outputs – yes and no, true or false, or 0 and 1. NAND itself is short for Not-And.
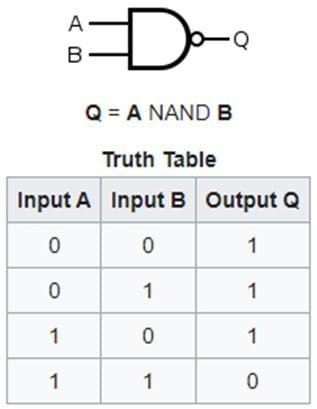
A NAND gate returns one as a result in every input case, other than if all input elements are also 1. So, if 0 and 0, or 0 and 1 are put in, the output is 1. Only if the input is 1 and 1 does the NAND gate return a 0.
Tip: The inputs and outputs are sometimes considered high and low rather than true or false. Naturally, Low is 0, and High is 1. It’s functionally irrelevant what they are called – the important parts are the values of 0 and 1.
NAND gates aren’t limited to two inputs either – while they need to have a minimum of two, they can process more. The logic behind it remains the same – unless all inputs are 1, the gate will always return one, no matter how many inputs there are. The standard setups are 2-, 3-, 4 and 8-input gates. These versions are actively used in semiconductors available on the market.
Use of NAND gates
Along with the similar but different setup NOR gates, NAND gates are essential in modern digital electronics. They can be used to express absolutely any Boolean function if they are combined correctly. A Boolean function is a function that is based on two values – once again, 0 and 1. Boolean functions and logic gates like NAND or NOR are essential in working various computer parts.
Their ability to express other functions is called ‘functional completeness’ – and as mentioned, Boolean functions such as AND, OR, XNOR, and NOT can be described entirely through NAND gates. You could build an entire computer processor from nothing but NAND gates. That isn’t the case since it would be expensive, inefficient, and not up to par as far as performance goes… however it is possible from a technical standpoint!
These gates are essential parts of computer hardware – they are found in most semiconductors used as a base component for PC parts, for example. When placed on an integrated circuit or PCB, a NAND gate will take up three pads – two for the two input values (or more if the gate needs to process more than two) and one for the resulting output.
Theoretical NAND
Although, in most cases, a reference to NAND will mean the physical gates used in the building of processors or SSDs, that isn’t always the case – NAND is also the name for the corresponding Boolean function. In this case, it means a mathematical function proven in 1913 by Henry Sheffer. The theoretical version is often called NAND logic to distinguish it from the NAND gates mentioned above.
This logic – and the corresponding function are expressed like this:
NAND Diagram and Truth Table
The truth table explains the possible in- and output options mentioned above. All combinations other than all 1s return a 1 – and all 1 inputs return 0 as an output.
Different combinations of NAND logic (or gates) can be used to create other Boolean mathematical functions. As mentioned, this functional completeness means that NAND logic is enough to build any other logic gate. This is done by repeating using multiple NAND gates in specific configurations. One of the more complicated possible Boolean functions is XNOR. To create one with only NAND functions, five must be structured together and connected in a specific way to achieve the desired output. This is what that would look like:

While the diagram for the XNOR gate in and of itself is far simpler, both of these options will deliver the same output – Q – from the same inputs – A and B. Different ways of assembling NAND gates are needed to create other types of functional gates both in physical semiconductors and in theoretical mathematic problems.
Conclusion
NAND is a logic gate; it stands for Not-And. A NAND gate is the logical inverse of an AND gate. An AND gate only returns true if all inputs are true. Conversely, a NAND gate is always true unless all inputs are true. NAND gates have a property called functional completeness that allows them to be combined to create all other logic gates. NAND gates are core components of processors as well as flash memory.



